题目内容
2.(1)计算:(-2)2sin60°-(-$\frac{1}{2}$)•$\sqrt{12}$-(-$\sqrt{3}$)0;(2)已知x,y满足方程组$\left\{\begin{array}{l}{x+2y=7}\\{2x+y=5}\end{array}\right.$,求2x-2y的值.
分析 (1)原式利用乘方的意义,特殊角的三角函数值,二次根式性质,以及零指数幂法则计算即可得到结果;
(2)方程组两方程相减求出x-y的值,代入原式计算即可得到结果.
解答 解:(1)原式=4×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×2$\sqrt{3}$-1=3$\sqrt{3}$-1;
(2)$\left\{\begin{array}{l}{x+2y=7①}\\{2x+y=5②}\end{array}\right.$,
②-①得:x-y=-2,
则2x-2y=2(x-y)=-4.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.如果一元一次不等式组$\left\{\begin{array}{l}{x>3}\\{x≥a}\end{array}\right.$的解集为x>3,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
7.若m>n,下列不等式不一定成立的是( )
| A. | m+2>n+2 | B. | 2m>2n | C. | -2m<-2n | D. | m2>n2 |
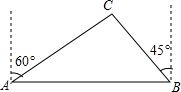 某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由.
某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由. 如图:AB为的⊙0弦;点D和C在⊙0上;且有AD=BC,求证:△ABD≌△BAC.
如图:AB为的⊙0弦;点D和C在⊙0上;且有AD=BC,求证:△ABD≌△BAC.