题目内容
15. 如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
如图所示,一次函数y=-$\frac{2}{3}$x+2的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰直角△ABC,∠BAC=90°,试求经过B、C两点的直线的函数表达式.
分析 根据坐标轴上的点的坐标特征,结合一次函数的解析式求出A、B两点的坐标,得出OA=3,OB=2,作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,AD=OB,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
解答 解:一次函数y=-$\frac{2}{3}$x+2中,
令y=0,解得x=3.
则点A的坐标是(3,0).
令x=0得y=2.
则点B的坐标是(0,2).
∴OA=3,OB=2,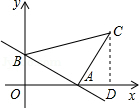 作CD⊥x轴于点D.
作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
$\left\{\begin{array}{l}{∠BOA=∠CDA=90°}\\{∠ACD=∠BAO}\\{AB=AC}\end{array}\right.$,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,
∴OD=OA+AD=5.
则点C的坐标是(5,3).
设直线BC的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{b=2}\\{5k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=2}\end{array}\right.$.
则直线BC的解析式是:y=$\frac{1}{5}$x+2.
点评 本题考查了用待定系数法求一次函数的解析式、一次函数图象上点的坐标特征、等腰三角形的性质以及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.按下面的程序计算:

当输入x=100时,输出结果是299;当输入x=50时,输出结果是466;如果输入x的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

当输入x=100时,输出结果是299;当输入x=50时,输出结果是466;如果输入x的值是正整数,输出结果是257,那么满足条件的x的值最多有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列判断中错误的是( )
| A. | 有两角和一边对应相等的两个三角形全等 | |
| B. | 有两边和一角对应相等的两个三角形全等 | |
| C. | 有两边和其中一边上的中线对应相等的两个三角形全等 | |
| D. | 有一边对应相等的两个等边三角形全等 |
5.下列方程变形中,正确的是( )
| A. | 方程3x-2=2x+1,移项得,3x-2x=-1+2 | |
| B. | 方程3-x=2-5( x-1),去括号得,3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}t=\frac{3}{2}$,系数化为1得,t=1 | |
| D. | 方程$\frac{x-1}{0.2}-\frac{x}{0.5}=1$,去分母得,5( x-1)-2x=1 |
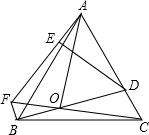 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D,且∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,过点D作DE⊥AF于点E,则DE=$\frac{5\sqrt{5}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D,且∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,过点D作DE⊥AF于点E,则DE=$\frac{5\sqrt{5}}{3}$.