题目内容
20.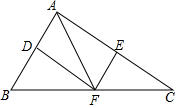 如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且BC=2AF.
如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,且BC=2AF.(1)求证:四边形ADFE为矩形;
(2)若∠C=30°,AF=2,写出矩形ADFE的周长.
分析 (1)连接DE.根据三角形的中位线的性质即可得到结论;
(2)根据矩形的性质得到∠BAC=∠FEC=90°,解直角三角形即可得到结论.
解答 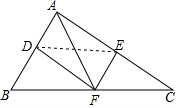 (1)证明:连接DE.
(1)证明:连接DE.
∵E,F分别是边AC,BC的中点,
∴EF∥AB,EF=$\frac{1}{2}$AB,
∵点D是边AB的中点,
∴AD=$\frac{1}{2}$AB.
∴AD=EF.
∴四边形ADFE为平行四边形;
由点D,E分别是边AB,AC的中点,
∴DE=$\frac{1}{2}$BC.
∵BC=2AF,
∴DE=AF,
∴四边形ADFE为矩形;
(2)解:∵四边形ADFE为矩形,
∴∠BAC=∠FEC=90°,
∵AF=2,
∴BC=4,CF=2,
∵∠C=30°,
∴AC=2$\sqrt{3}$,CE=$\sqrt{3}$,EF=1,
∴AE=$\sqrt{3}$,
∴矩形ADFE的周长=2$\sqrt{3}$+2.
点评 本题考查了矩形的性质和判定,三角形的中位线的性质,解直角三角形,熟练掌握矩形的判定和性质是解题的关键.

练习册系列答案
相关题目
20.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=-$\frac{2}{x}$的图象上,则( )
| A. | a<b<0 | B. | b<a<0 | C. | a<0<b | D. | b<0<a |
11.反比例函数y=$\frac{k}{x}$(k≠0)图象上的两个点A(x1,y1),B(x2,y2),当x1<x2<0时,y1>y2,那么一次函数y=-2kx+k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( )
| A. | ab>0 | B. | a-b>0 | C. | a+b>0 | D. | a2+b>0 |
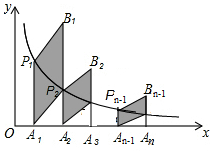 如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)
如图,分别过反比例函数y=$\frac{3}{x}$(x>0)图象上的点P1(1,y1),P2(2,y2)…Pn(n,yn)作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An-1Pn,再以A1P1,A1P2为一组邻边作平行四边形A1P1B1P2,以A2P2,A2P3为邻边作平行四边形A2P2B2P3,以此类推,则B1的纵坐标为$\frac{9}{2}$,Bn的纵坐标为$\frac{6n+3}{n(n+1)}$(用含n的代数式表示)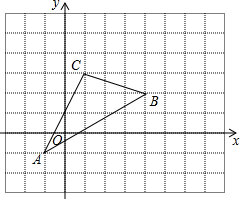 如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).
如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).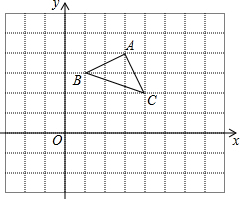 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-1,1),现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点,请画出平移后的△A′B′C′,并直接写出点B′、C′的坐标:B′(-3,0)、C′(0,-1).
在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(-1,1),现将△ABC平移,使点A变换为A′,点B′、C′分别是B、C的对应点,请画出平移后的△A′B′C′,并直接写出点B′、C′的坐标:B′(-3,0)、C′(0,-1).