题目内容
2.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再由各点横坐标的值即可得出结论.
解答 解:∵反比例函数y=$\frac{3}{x}$中k=3>0,
∴此函数图象的两个分支分别位于一三象限,并且在每一象限内,y随x的增大而减小.
∵A(-5,y1),B(-3,y2),C(2,y3)三点都在反比例函数y=$\frac{3}{x}$的图象上,
∴A、B在第三象限,点C在第一象限,
∴y2<y1<y3.
故选D.
点评 本题考查的是反比例函数函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.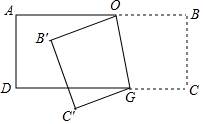 如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
 如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |

 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x-2y+z的值是( )
如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x-2y+z的值是( )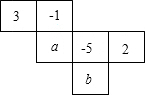 如图,是一个正方体纸盒展开图,在它的六个面上分别标有数字3、-1、a、-5、2、b,将它沿虚线折成正方形后,则a对面上的数字是2,b对面上的数字是-1.
如图,是一个正方体纸盒展开图,在它的六个面上分别标有数字3、-1、a、-5、2、b,将它沿虚线折成正方形后,则a对面上的数字是2,b对面上的数字是-1. 如图,在△ABC中,D、E分别在AB与AC上,且AD=5,DB=7,AE=6,EC=4,△ADE与△ACB相似吗?请说明理由.
如图,在△ABC中,D、E分别在AB与AC上,且AD=5,DB=7,AE=6,EC=4,△ADE与△ACB相似吗?请说明理由. 如图,已知数轴上A、B两点所表示的数分别为-2和8.
如图,已知数轴上A、B两点所表示的数分别为-2和8. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,CD=10,EM=25.求⊙O的半径.
如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,CD=10,EM=25.求⊙O的半径.