题目内容
7. 如图,在△ABC中,D、E分别在AB与AC上,且AD=5,DB=7,AE=6,EC=4,△ADE与△ACB相似吗?请说明理由.
如图,在△ABC中,D、E分别在AB与AC上,且AD=5,DB=7,AE=6,EC=4,△ADE与△ACB相似吗?请说明理由.
分析 相似,利用计算两边的比相等,夹角是公共角,可得两三角形相似.
解答 解:△ADE∽△ACB,理由是:
∵AD=5,DB=7,AE=6,EC=4,
∵$\frac{AD}{AC}$=$\frac{5}{6+4}$=$\frac{1}{2}$,$\frac{AE}{AB}$=$\frac{6}{7+5}$=$\frac{1}{2}$,
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
又∵∠A=∠A,
∴△ADE∽△ACB.
点评 本题考查了三角形相似的判定,熟练掌握相似三角形的判定方法是关键,利用两边的比相等且夹角相等证明两三角形相似时,注意边的对应关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列计算正确的是( )
| A. | 3a+2b=5ab | B. | 5y-3y=2 | C. | 3x2y-2yx2=x2y | D. | -3x+5x=-8x |
18.已知a=25000用科学记数法表示为2.5×4,那么a2用科学记数法表示为( )
| A. | 62.5×108 | B. | 6.25×109 | C. | 6.25×108 | D. | 6.25×107 |
2.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
12. 如图,在Rt△ABC中,∠C=90°,已知sinA=$\frac{3}{4}$,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,已知sinA=$\frac{3}{4}$,则cosB的值为( )
 如图,在Rt△ABC中,∠C=90°,已知sinA=$\frac{3}{4}$,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,已知sinA=$\frac{3}{4}$,则cosB的值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
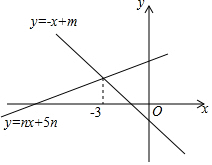 如图,直线y=-x+m与y=nx+5n(n≠0)的交点横坐标为-3,则关于的不等式-x+m>nx+5n>0的整数解是-4.
如图,直线y=-x+m与y=nx+5n(n≠0)的交点横坐标为-3,则关于的不等式-x+m>nx+5n>0的整数解是-4. 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠BOF=30°,则∠AOC=80°.
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠BOF=30°,则∠AOC=80°.