题目内容
12. 如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,CD=10,EM=25.求⊙O的半径.
如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,CD=10,EM=25.求⊙O的半径.
分析 根据垂径定理得出EM⊥CD,则CM=DM=2,在Rt△COM中,有OC2=CM2+OM2,进而可求得半径OC.
解答 解:如图,连接OC,
∵M是弦CD的中点,EM过圆心O,
∴EM⊥CD.
∴CM=MD.
∵CD=10,
∴CM=5.
设OC=x,则OM=25-x,
在Rt△COM中,根据勾股定理,得
52+(25-x)2=x2.
解得 x=13.
∴⊙O的半径为13.
点评 此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形.

练习册系列答案
相关题目
2.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
7.下列事件中,是必然事件的是( )
| A. | 明天太阳从东方升起 | |
| B. | 射击运动员射击一次,命中靶心 | |
| C. | 随意翻到一本书的某页,这页的页码是奇数 | |
| D. | 经过有交通信号灯的路口,遇到红灯 |
4.已知M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直,平行 | D. | 平行,垂直 |
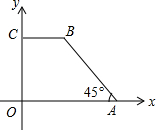 如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°.
如图,在平面直角坐标系中有一个四边形OABC,其中CB∥x轴,OC=3,BC=2,∠OAB=45°.