题目内容
如图1,双曲线y=
(x>0)经过点A(2,1),过点P(a+1,a-1)(a>1)作x轴的平行线分别交双曲线y=
(x<0)和y=
(x>0)于M、N两点,交y轴于T点.
(1)求m的值;
(2)如图2,若MT=2NT,求k的值;
(3)是否存在实数a,使得S△AMN=3S△APN?
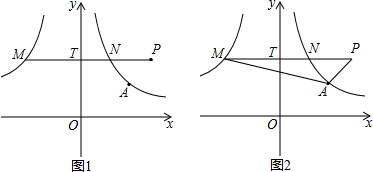
| m |
| x |
| k |
| x |
| m |
| x |
(1)求m的值;
(2)如图2,若MT=2NT,求k的值;
(3)是否存在实数a,使得S△AMN=3S△APN?
考点:反比例函数综合题
专题:
分析:(1)把A的坐标代入双曲线的解析式即可求解;
(2)利用a表示出NT的长,则MT即可求得,从而求得M的坐标,代入解析式即可求得k的值;
(3)S△AMN=3S△APN,则MN=3NT,据此即可得到一个关于a的方程,从而求解.
(2)利用a表示出NT的长,则MT即可求得,从而求得M的坐标,代入解析式即可求得k的值;
(3)S△AMN=3S△APN,则MN=3NT,据此即可得到一个关于a的方程,从而求解.
解答:解:(1)把A(2,1)代入y=
得:m=2;
(2)在y=
中,令y=a-1,解得:x=
,则NT=
,
则MT=
,
M的坐标是(
,a-1),代入y=
得:k=-4;
(3)PN=(a-1)-
=
,
MN=3NT=
,
根据题意得:
=3×
,
解得:a=3或-1(舍去).
则a=3.
| m |
| x |
(2)在y=
| 2 |
| x |
| 2 |
| a-1 |
| 2 |
| a-1 |
则MT=
| 4 |
| a-1 |
M的坐标是(
| -4 |
| a-1 |
| k |
| x |
(3)PN=(a-1)-
| 2 |
| a-1 |
| (a-1)2-2 |
| a-1 |
MN=3NT=
| 6 |
| a-1 |
根据题意得:
| 6 |
| a-1 |
| (a-1)2-2 |
| a-1 |
解得:a=3或-1(舍去).
则a=3.
点评:本题考查了待定系数法求函数的解析式,正确利用a表述出NT和MN的长是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
为了丰富人民的生活,泗阳县政府投资110000000元兴建了生态公园,110000000元用科学记数法表示应为( )
| A、1.169×109元 |
| B、1.1×108元 |
| C、11×108元 |
| D、0.11×109元 |
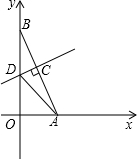 已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D.
已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D. 如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角.
如图所示,已知∠AOB=∠COD=90°,找出图中其他相等的角及图中互余的角.