题目内容
6.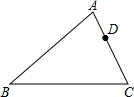 如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为( )| A. | $\frac{8}{3}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{8}{3}$或$\frac{3}{2}$ |
分析 由∠A是公共角,分别从当$\frac{AE}{AB}=\frac{AD}{AC}$,即$\frac{AE}{8}=\frac{2}{6}$时,△AED∽△ABC与当$\frac{AE}{AC}=\frac{AD}{AB}$,即$\frac{AE}{6}=\frac{2}{8}$时,△ADE∽△ABC,去分析求解即可求得答案.
解答 解:∵∠A是公共角,
∴当$\frac{AE}{AB}=\frac{AD}{AC}$,即$\frac{AE}{8}=\frac{2}{6}$时,△AED∽△ABC,
解得:AE=$\frac{8}{3}$;
当$\frac{AE}{AC}=\frac{AD}{AB}$,即$\frac{AE}{6}=\frac{2}{8}$时,△ADE∽△ABC,
解得:AE=$\frac{3}{2}$,
∴AE的长为:$\frac{8}{3}$或$\frac{3}{2}$.
故选D.
点评 此题考查了相似三角形的判定.注意分类讨论思想的应用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.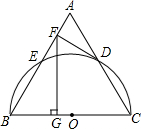 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
 如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )| A. | 4 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.在运动会上,成绩是按点到直线的距离来评定的有( )
| A. | 跳远 | B. | 跳高 | C. | 掷铅球 | D. | 掷标枪 |
 一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )
一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )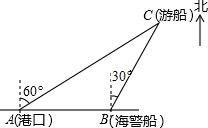 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示). 如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.