题目内容
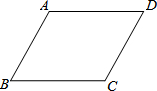 已知:如图,AB=DC,AD=BC.(提示:连接BD)
已知:如图,AB=DC,AD=BC.(提示:连接BD)求证:(1)∠A=∠C;
(2)AB∥CD,AD∥BC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)连接BD,根据SSS推出△ABD和△CDB全等即可;
(2)根据全等三角形的性质得出∠ADB=∠CBD,∠ABD=∠CDB,根据平行线的判定得出即可.
(2)根据全等三角形的性质得出∠ADB=∠CBD,∠ABD=∠CDB,根据平行线的判定得出即可.
解答:证明:(1)连接BD,
∵在△BAD和△DCB中
∴△BAD≌△DCB(SSS),
∴∠A=∠C;
(2)∵△BAD≌△DCB,
∴∠ADB=∠CBD,∠ABD=∠CDB,
∴AB∥CD,AD∥BC.

∵在△BAD和△DCB中
|
∴△BAD≌△DCB(SSS),
∴∠A=∠C;
(2)∵△BAD≌△DCB,
∴∠ADB=∠CBD,∠ABD=∠CDB,
∴AB∥CD,AD∥BC.
点评:本题考查了全等三角形的性质和判定,平行线的判定的应用,解此题的关键是推出△BCE≌△CAD,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
以下四个图中对称轴条数最多的一个图形是( )
A、 |
B、 |
C、 |
D、 |
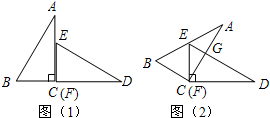 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为
如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为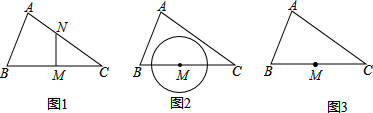
 如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE= 如图,在矩形ABCD中,点O在对角AC上,以OA长为半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.求证:CE是⊙O的切线.
如图,在矩形ABCD中,点O在对角AC上,以OA长为半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.求证:CE是⊙O的切线.