题目内容
7.如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D;(1)如图1,求证:AC平分∠DAB;
(2)如图2,延长DC交AB的延长线于G,AD交⊙O于M,连接MC,当四边形GCMB是平行四边形时,求证:AM=2MD;
(3)如图3,延长DC交AB的延长线于G,若tan∠DAC=$\frac{1}{2}$,BG=5,求⊙O的半径.
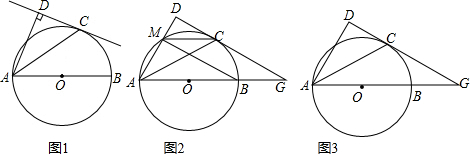
分析 (1)首先连接OC,由AD和过点C的切线互相垂直,易证得OC∥AD,继而证得AC平分∠DAB;
(2)由四边形GCMB是平行四边形,可得MC∥AG,即可证得四边形OAMC是平行四边形,则可得AG=3MC,且△DMC∽△DAG,继而证得结论;
(3)首先连接BC,由(1)可得∠DAC=∠BAC,即可得$\frac{BC}{AC}$=$\frac{1}{2}$,易证得△GCB∽△GAC,然后由相似三角形的对应边成比例,求得CG与AG的长,继而求得答案.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵CD是⊙O切线,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,
即AC平分∠DAB; (2)证明:连接OC,由(1)得:OC∥AD,
(2)证明:连接OC,由(1)得:OC∥AD,
∵四边形GCMB是平行四边形,
∴CM∥AG,CM=BG,
∴四边形OAMC是平行四边形,
∴MC=OA,
即MC=OA=OB=BG=$\frac{1}{3}$AG,
∵MC∥AG,
∴△DMC∽△DAG,
∴$\frac{DM}{DA}$=$\frac{MC}{AG}$=$\frac{1}{3}$,
∴$\frac{DM}{AM}$=$\frac{1}{2}$,
即AM=2MD; (3)解:连接BC,
(3)解:连接BC,
∵CD是⊙O切线,
∴∠GCB=∠GAC,
∵∠G是公共角,
∴△GBC∽△GCA,
∴$\frac{CG}{AG}$=$\frac{BG}{CG}$=$\frac{BC}{AC}$,
∵AB是直径,
∴∠ACB=90°,
∵∠DAC=∠BAC,
∴tan∠DAC=tan∠BAC=$\frac{BC}{AC}$=$\frac{1}{2}$,
∵BG=5,
∴CG=2BG=10,
∴AG=2CG=20,
∴AB=AG-BG=15,
∴⊙O的半径为:7.5.
点评 此题属于圆的综合题,考查了切线的性质、相似三角形的判定与性质、平行四边形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=2 | D. | 直线x=-2 |
| A. | x2+x4=x6 | B. | 2xy+3xy=5xy | C. | (x3)2=x6 | D. | x6÷x3=x3 |
 如图1是一个正方体的展开图,若将这个展开图再折成正方体放在桌面上,如图2所示,则从上面看到的面为( )
如图1是一个正方体的展开图,若将这个展开图再折成正方体放在桌面上,如图2所示,则从上面看到的面为( ) 如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数.
如图,AD∥BC,BD⊥BC,若∠ABD=25°,求∠A的度数.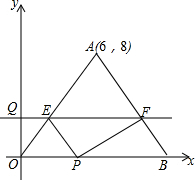 如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.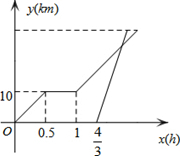 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.