题目内容
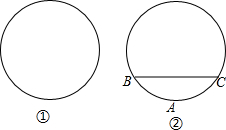 某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径.
某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径.(1)小杰先找圆心,再量半径.请你在图①中,用尺规作图的方法帮小杰找到该广场的圆心O(不写作法,保留作图痕迹);
(2)小浩在广场边(如图②)选取A、B、C三根石柱,量得A、B之间的距离与A、C之间的距离相等,并测得BC长为240米,A到BC的距离为5米.请你帮他求出广场的半径(结果精确到米).
考点:垂径定理的应用,勾股定理
专题:
分析:(1)作出弦的垂直平分线,再结合垂径定理推论得出圆心位置;
(2)设圆心为O,连结 OA、OB,OA交BC于D,根据A、B之间的距离与A、C之间的距离相等,得出
=
,从而得出BD=DC=
BC,再根据勾股定理得出OB2=OD2+BD2,设OB=x,即可求出广场的半径.
(2)设圆心为O,连结 OA、OB,OA交BC于D,根据A、B之间的距离与A、C之间的距离相等,得出
 |
| AB |
 |
| AC |
| 1 |
| 2 |
解答: 解:(1)如图所示,在圆中作任意2条弦的垂直平分线,由垂径定理可知这2条垂直平分线必定与圆的2条直径重合,
解:(1)如图所示,在圆中作任意2条弦的垂直平分线,由垂径定理可知这2条垂直平分线必定与圆的2条直径重合,
所以交点O即为所求;
(2)设圆心为O,连结 OA、OB,OA交BC于D,
∵AB=AC,
∴
=
,
∴OA⊥BC,
∴BD=DC=
BC=120(米),
由题意DA=5,
在Rt△BDO中,
OB2=OD2+BD2,
设OB=x,
则x2=(x-5)2+1202,
解得:10x=14425,
x≈1443,
答:广场的半径1443米.
 解:(1)如图所示,在圆中作任意2条弦的垂直平分线,由垂径定理可知这2条垂直平分线必定与圆的2条直径重合,
解:(1)如图所示,在圆中作任意2条弦的垂直平分线,由垂径定理可知这2条垂直平分线必定与圆的2条直径重合,所以交点O即为所求;
(2)设圆心为O,连结 OA、OB,OA交BC于D,
∵AB=AC,
∴
 |
| AB |
 |
| AC |
∴OA⊥BC,
∴BD=DC=
| 1 |
| 2 |
由题意DA=5,

在Rt△BDO中,
OB2=OD2+BD2,
设OB=x,
则x2=(x-5)2+1202,
解得:10x=14425,
x≈1443,
答:广场的半径1443米.
点评:此题主要考查了垂径定理的应用,用到的知识点是垂径定理、勾股定理、弧、弦、圆周角之间的关系,熟练利用勾股定理得出AO的长是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
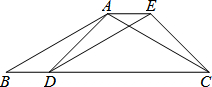 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC. 如图,在四边形ABCD中,已知AB∥CD,∠A=∠B,DA∥CE.
如图,在四边形ABCD中,已知AB∥CD,∠A=∠B,DA∥CE.