题目内容
15. (1)如图,在△ABC中,AD⊥BC,∠1=∠B,求证:△ABC是直角三角形.
(1)如图,在△ABC中,AD⊥BC,∠1=∠B,求证:△ABC是直角三角形.(2)你在(1)的证明过程中,运用了哪两个互逆的真命题?
分析 (1)根据直角三角形两锐角互余可得∠1+∠C=90°,然后求出∠B+∠C=90°,再根据直角三角形的定义证明即可;
(2)根据直角三角形两锐角互余解答.
解答 (1)证明:∵AD⊥BC,
∴∠1+∠C=90°,
∵∠1=∠B,
∴∠B+∠C=90°,
∴△ABC是直角三角形;
(2)解:利用了直角三角形两锐角互余,两锐角互余的三角形是直角三角形.
点评 本题考查了直角三角形两锐角互余的性质,直角三角形的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.不等式组$\left\{\begin{array}{l}{x+\frac{x+1}{2}>\frac{2x-9}{3}-\frac{x-3}{6}}\\{-\frac{1}{2}(1-2x)>1}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x>$\frac{3}{2}$ | C. | -3<x<$\frac{3}{2}$ | D. | 无解 |
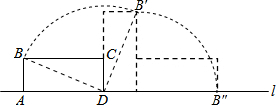 如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.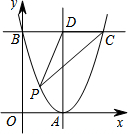 如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4.
如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B.过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(P不与B,C重合),连结PC,PD,则△PCD面积的最大值是4.