题目内容
9.请观察下列等式的规律:$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),
$\frac{1}{5×7}$=$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$),$\frac{1}{7×9}$=$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$),
…
则$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{99×101}$=$\frac{50}{101}$.
分析 观察算式可知$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)(n为非0自然数),把算式拆分再抵消即可求解.
解答 解:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{99×101}$
=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)+…+$\frac{1}{2}$($\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{2}$(1-$\frac{1}{101}$)
=$\frac{1}{2}$×$\frac{100}{101}$
=$\frac{50}{101}$.
故答案为:$\frac{50}{101}$.
点评 考查了规律型:数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)(n为非0自然数).

练习册系列答案
相关题目
14.计算(-2a2b)3的结果是( )
| A. | -6a6b3 | B. | -8a6b3 | C. | 8a6b3 | D. | -8a5b3 |
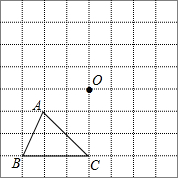 如图,在方格网中已知格点△ABC和点O.
如图,在方格网中已知格点△ABC和点O. 如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=$\frac{k}{x}$(0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(-2,0).
如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=$\frac{k}{x}$(0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(-2,0). 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.