题目内容
1. 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.
分析 根据三角形内角和定理求出∠B,根据折叠求出∠ECD和∠CED,根据三角形内角和定理求出即可.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠A=26°,
∴∠B=64°,
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠CED=∠B=64°,
∴∠CDE=180°-∠ECD-∠CED=71°,
故答案为:71°.
点评 本题考查了折叠的性质,三角形内角和定理的应用,能求出∠CED和∠ECD的度数是解此题的关键,注意:折叠后的两个图形全等.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
16.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
13.在天水市汉字听写大赛中,10名学生得分情况如表
那么这10名学生所得分数的中位数和众数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
4.若函数$y=(m-1){x^{{m^2}-2}}$为反比例函数,则m的值为( )
| A. | ±1 | B. | 1 | C. | $\sqrt{3}$ | D. | -1 |
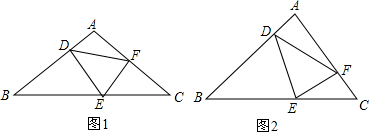
 如图,△ACD≌△ECD,△CEF≌△BEF,∠ACB=90°,CD⊥AB
如图,△ACD≌△ECD,△CEF≌△BEF,∠ACB=90°,CD⊥AB