题目内容
9.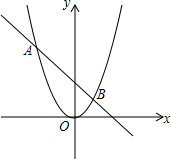 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx+c=0的解为无解.
分析 把A坐标代入抛物线解析式求出a的值,把A与B坐标代入直线解析式求出b与c的值,将a,b,c的值代入方程,求出解即可.
解答 解:把A(-2,4)代入抛物线解析式得:4=4a,即a=1,
把a=1代入得:y=x2,
把A(-2,4)与B(1,1)代入直线解析式得:$\left\{\begin{array}{l}{-2b+c=4}\\{b+c=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-1}\\{c=2}\end{array}\right.$,即直线解析式为y=-x+2,
可得方程x2+x+2=0,
∵△=1-8=-7<0,
∴此方程无解.
故答案为:无解.
点评 此题考查了抛物线与x轴的交点,待定系数法求函数解析式,以及一元二次方程的解法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若函数y=(k2-1)x2-2(k+1)x+1(k为常数)的图象与x轴没有公共点,则k的取值范围是( )
| A. | k<-1 | B. | k<0,且k≠-1 | C. | k≤-1 | D. | k=1,或k≤-1 |
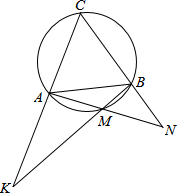 如图,已知等边△ABC内接于圆,圆的半径为$\frac{\sqrt{3}}{2}$,在劣弧AB上取异于A、B的点M.如果设直线AC与BM相交于K,直线CB与AM相交于点N,则线段AK•BN的值为$\frac{9}{4}$.
如图,已知等边△ABC内接于圆,圆的半径为$\frac{\sqrt{3}}{2}$,在劣弧AB上取异于A、B的点M.如果设直线AC与BM相交于K,直线CB与AM相交于点N,则线段AK•BN的值为$\frac{9}{4}$.