题目内容
20.1883年,德国数学家格奥尔格•康托尔引入位于一条线段上的一些点的集合,他的做法如下:取一条长度为1的线段,将它三等分,去掉中间一段,余下两条线段,达到第1阶段;将剩下的两条线段再分别三等分,各去掉中间一段,余下四条线段,达到第2阶段;再将剩四条线段,分别三等分,分别去掉中间一段,余下八条线段,达到第3阶段;…;这样的操作一直继续下去,在不断分割舍弃过程中,所形成的线段数目越来越多,把这种分形,称做康托尔点集.下图是康托尔点集的最初几个阶段,当达到第5个阶段时,余下的线段的长度之和为($\frac{2}{3}$)5;当达到第n个阶段时(n为正整数),余下的线段的长度之和为($\frac{2}{3}$)n.

分析 根据题意可知:当第一阶段时,余下线段之和为$\frac{2}{3}$,当第二阶段时,余下线段之和为:$\frac{4}{9}$=($\frac{2}{3}$)2,当第三阶段时,余下线段之和为:$\frac{8}{27}$=($\frac{2}{3}$)3,
解答 解:根据分析可知:当达到第5阶段时,余下的线段之和为$(\frac{2}{3})^{5}$,
当达到n的阶段时,余下线段之和为($\frac{2}{3}$)n,
故答案为:($\frac{2}{3}$)5;($\frac{2}{3}$)n
点评 本题考查数字规律,注意找出前面几种情况,然后总结其中的规律

练习册系列答案
相关题目
10.下列说法错误的是( )
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1不是单项式 | ||
| C. | -$\frac{2}{3}$πxy2的系数是-$\frac{2}{3}$π | D. | -22xyb2的次数是6 |
 如图所示:
如图所示:
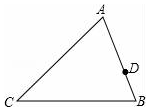 如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.
如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.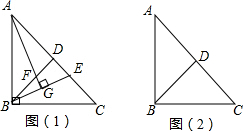 如图(1),已知等腰直角△ABC中,BD为斜边上的中线,E为DC上的一点,且AG⊥BE于G,AG交BD于F.
如图(1),已知等腰直角△ABC中,BD为斜边上的中线,E为DC上的一点,且AG⊥BE于G,AG交BD于F.