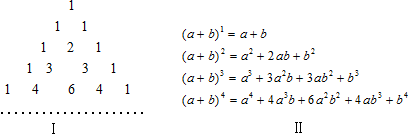题目内容
12.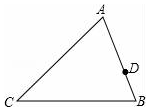 如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.
如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=$\frac{2}{3}$AB,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于10或6.4.
分析 根据相似三角形对应边成比例得出$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{AC}$=$\frac{AE}{AB}$,再代值计算即可.
解答 解:∵△ABC∽△ADE,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{AC}$=$\frac{AE}{AB}$,
∵AD=$\frac{2}{3}$AB,AB=12,
∴AD=8,
∵AC=15,
∴$\frac{8}{12}$=$\frac{AE}{15}$或$\frac{8}{15}$=$\frac{AE}{12}$,
解得:AE=10或6.4.
故答案为10或6.4
点评 此题考查了相似三角形的判定与性质,根据相似得到相应的线段的关系是解决本题的关键.

练习册系列答案
相关题目

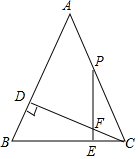 已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论.
已知:在△ABC中,AB=AC,CD是AB边上的高,点P是AC边上任意一点(不与点A、点C重合)过点P作PE⊥BC,垂足为E,交CD于点F.若AD=CD,探究线段PF、CE之间的数量关系,并证明你的结论. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.