题目内容
5．如果am=3，a2m+n=36，则an的值是4．分析 先将a2m+n变形为（am）2×an，然后结合幂的乘方与积的乘方的概念和运算法则进行求解即可．
解答 解：∵am=3，a2m+n=36=（am）2×an，
∴an
=a2m+n÷（am）2
=36÷32
=36÷9
=4．
故答案为：4．
点评 本题考查了幂的乘方与积的乘方，解答本题的关键在于熟练掌握该知识点的概念和运算法则．
练习册系列答案
备战中考寒假系列答案
相关题目
20．已知函数y=-$\frac{1}{2}$x+2，当-1＜x≤1时，则y的取值范围（ ）
| A． | -$\frac{5}{2}$＜y≤$\frac{3}{2}$ | B． | $\frac{3}{2}$＜y＜$\frac{5}{2}$ | C． | $\frac{3}{2}$＜y≤$\frac{5}{2}$ | D． | $\frac{3}{2}$≤y＜$\frac{5}{2}$ |
13．
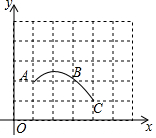如图，在平面直角坐标系中，过格点A，B，C作一圆弧，则该弧的圆心的坐标为（ ）
如图，在平面直角坐标系中，过格点A，B，C作一圆弧，则该弧的圆心的坐标为（ ）| A． | （1，0） | B． | （2，0） | C． | （2.5，0） | D． | （2.5，1） |
10．下列命题的逆命题是真命题的是（ ）
| A． | 同位角相等 | B． | 对顶角相等 | ||
| C． | 钝角三角形有两个锐角 | D． | 两直线平行，内错角相等 |