题目内容
3. 如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
如图,在正方形ABCD中,E,F,G,H分别在它的四条边上,且AE=BF=CG=DH.四边形EFGH是什么特殊四边形?你是如何判断的?
分析 是正方形.可通过证明△AEH,△DHG,△CGF,△BFE全等,先得出四边形EFGH是菱形,再证明四边形EFGH中一个内角为90°,从而得出四边形EFGH是正方形的结论.
解答 解:四边形EFGH是正方形.
证明:∵AE=BF=CG=GH,
∴AH=DG=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△DHG≌△CGF≌△BFE,
∴EF=EH=HG=GF,∠EHA=∠HGD.
∴四边形EFGH是菱形.
∵∠EHA=∠HGD,∠HGD+∠GHD=90°,
∴∠EHA+∠GHD=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
点评 本题主要考查了全等三角形的判定及性质和正方形的性质和判定,熟练掌握判定定理是解答此题的关键.

练习册系列答案
相关题目
8.在Rt△ABC中,∠A=90°,且tanB=$\frac{3}{4}$,则下列各式中不成立的是( )
| A. | sinC=$\frac{4}{5}$ | B. | tanC=$\frac{3}{5}$ | C. | cotB=$\frac{4}{3}$ | D. | cosB=$\frac{4}{5}$ |
13. 如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
 如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )
如图,在一个长6m、宽3m、高2m的房间里放进一根竹竿,则这根竹竿最长为( )| A. | 4m | B. | 7m | C. | 2m | D. | 8m |
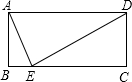 如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.
如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7. 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.