题目内容
14.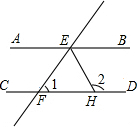 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EH平分∠BEF,若∠1=70°,
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EH平分∠BEF,若∠1=70°,∠2=125°.
分析 根据平行线的性质和角平分线定义求出∠FEH,再根据三角形外角性质计算即可.
解答  解:∵EH平分∠BEF,
解:∵EH平分∠BEF,
∴∠BEH=∠HEF,
∵AB∥CD,∠1=70°,
∴∠1+∠BEF=180°,即∠BEF=110°,
∴∠FEH=55°,
∴∠2=∠1+∠FEH=70°+55°=125°.
故答案为:125.
点评 本题主要考查了平行线的性质以及三角形外角性质,解题时注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
5.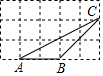 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
9.“$\frac{4}{9}$的平方根是$±\frac{2}{3}$”,用式子表示就是( )
| A. | $±\sqrt{\frac{4}{9}}=\frac{2}{3}$ | B. | $±\sqrt{\frac{4}{9}}=±\frac{2}{3}$ | C. | $\sqrt{\frac{4}{9}}=\frac{2}{3}$ | D. | $\sqrt{\frac{4}{9}}=±\frac{2}{3}$ |
4. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2∠1+∠2 | C. | 2∠A=∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
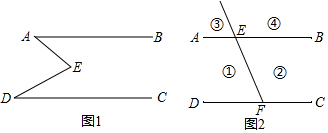
 如图,将矩形ABCD对折,折痕为MN,再把点B折叠在折痕MN上(点P),若AB=$\sqrt{3}$,则折痕AE的长为多少?
如图,将矩形ABCD对折,折痕为MN,再把点B折叠在折痕MN上(点P),若AB=$\sqrt{3}$,则折痕AE的长为多少?