题目内容
6.(1)计算:$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$÷$\sqrt{24}$(2)若a=1+$\sqrt{2}$,b=1-$\sqrt{2}$,求$\sqrt{{a}^{2}+{b}^{2}-3ab}$的值.
分析 (1)先化简二次根式,再计算即可;
(2)先计算a+b,再计算ab即可.
解答 解:(1)原式=$\sqrt{16}$-$\frac{1}{2}$
=4-$\frac{1}{2}$
=$\frac{7}{2}$;
(2)∵a=1+$\sqrt{2}$,b=1-$\sqrt{2}$,
∴a+b=2,ab=-1,
∴原式=$\sqrt{(a+b)^{2}-5ab}$
=$\sqrt{4-(-5)}$
=$\sqrt{9}$
=3.
点评 本题考查了二次根式的化简求值,掌握二次根式的化简是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
17.下列式子正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{-8}$=-2 | C. | $\sqrt{(-3)^{2}}$=-3 | D. | -$\sqrt{25}$=5 |
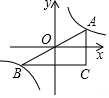 如图,过原点O的直线交双曲线y=$\frac{k}{x}$于A、B两点,分别过A、B向两坐标轴作垂线相交于点C,若△ABC的面积是12,则k=( )
如图,过原点O的直线交双曲线y=$\frac{k}{x}$于A、B两点,分别过A、B向两坐标轴作垂线相交于点C,若△ABC的面积是12,则k=( )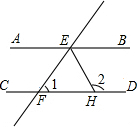 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EH平分∠BEF,若∠1=70°,
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EH平分∠BEF,若∠1=70°,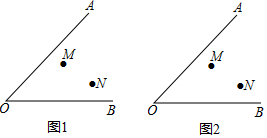
 如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.
如图,点P是y轴正半轴上的一动点,过点P作AB∥x轴,分别交反比例函数y=-$\frac{2}{x}$(x<0)与y=$\frac{1}{x}$(x>0)的图象于点A,B,连接OA,OB,则以下结论:①AP=2BP;②∠AOP=2∠BOP;③△AOB的面积为定值;④△AOB是等腰三角形,其中一定正确的有( )个.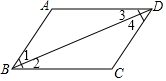 提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.