题目内容
5.解方程:(1)2(x-3)2=x2-9
(2)(x+1)(3x-1)=1.
分析 (1)等式的右边利用平方差公式进行因式分解;然后移项;再利用提取公因式法对等式的左边进行因式分解,即可求得x的值;
(2)先转化为一般式方程,然后利用求根公式进行解答.
解答 解:(1)由原方程,得
2(x-3)2=(x+3)(x-3),
(x-3)(2x-6-x-3)=0,
(x-3)(x-9)=0,
则x-3=0或x-9=0,
解得x1=3,x2=9;
(2)由原方程,得
3x2+2x-2=0,
故a=3,b=2,c=-2,
所以△=b2-4ac=22-4×3×(-2)=28,
所以x=$\frac{-2±\sqrt{28}}{6}$=$\frac{-1±\sqrt{7}}{3}$,
所以x1=$\frac{-1+\sqrt{7}}{3}$,x2=$\frac{-1-\sqrt{7}}{3}$.
点评 本题考查了公式法和因式分解法解一元二次方程.利用因式分解法解方程,实际上是把一元二次方程转化成2个一元一次方程后,再来求x的值,难度适中.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.下列命题是真命题的是( )
| A. | 如果两条直线被第三条直线所截,那么同位角相等 | |
| B. | 如果两个数的平方相等,那么这两个数也相等 | |
| C. | 平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交 | |
| D. | 从直线外一点到这条直线的垂线段,叫做这点到直线的距离 |
13.下列等式中,正确的是( )
| A. | 3a+2b=5ab | B. | 2(a-b)=2a-b | C. | (a-b)2=a2-b2 | D. | (-2a3)2=4a6 |
20.在平面直角坐标系中,若m为实数,则点(-2,m2+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.下列QQ表情中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
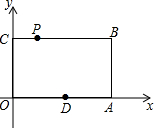 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).