题目内容
已知二次函数y=ax2+bx+c(a,b,c均为实数且a≠0)满足条件:对任意实数x都有y≥2x;且当0<x<2时,总有y≤
(x+1)2成立,则a+b+c的值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、1.5 | D、2.5 |
考点:二次函数的性质
专题:探究型
分析:根据对任意实数x都有y≥2x可知当x=1时,y≥2,由当0<x<2时,总有y≤
(x+1)2成立可知当x=1,y≤2,所以当x=1时,y=2,故二次函数y=ax2+bx+c经过(1,2)点,故可得出结论.
| 1 |
| 2 |
解答:解:∵对任意实数x都有y≥2x,
∴当x=1时,y≥2;
∵当0<x<2时,总有y≤
(x+1)2成立,
∴当x=1,y≤2,
∴当x=1时,y=2,
∴二次函数y=ax2+bx+c经过(1,2)点,
∴a+b+c=2.
故选B.
∴当x=1时,y≥2;
∵当0<x<2时,总有y≤
| 1 |
| 2 |
∴当x=1,y≤2,
∴当x=1时,y=2,
∴二次函数y=ax2+bx+c经过(1,2)点,
∴a+b+c=2.
故选B.
点评:本题考查的是二次函数的性质,根据题意得出当x=1时y的值是解答此题的关键.

练习册系列答案
相关题目
 用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(6)个图形中黑色瓷砖的块数为( )
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(6)个图形中黑色瓷砖的块数为( )| A、19 | B、16 | C、18 | D、22 |
 如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )
如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )| A、AB=CD |
| B、BE∥DF |
| C、∠B=∠D |
| D、BE=DF |
 给定直角三角形ABC,BC=a,CA=b,AB=c,∠ACB=90°,在BC边上取异于两端点的点P,过P作AB边的垂线,垂足为R,交AC的延长线于Q.
给定直角三角形ABC,BC=a,CA=b,AB=c,∠ACB=90°,在BC边上取异于两端点的点P,过P作AB边的垂线,垂足为R,交AC的延长线于Q.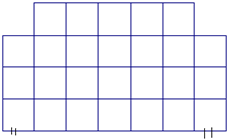 一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室?
一展览馆有26间展室,图中每个方格代表一个展室,每相邻展室有门相同,出口、入口如图所示.问:能否找到一条从入口到出口的参观路线,使不重复不遗漏地走过每一间展室?