题目内容
17.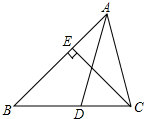 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADB的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
分析 根据AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,可得∠BAD和∠CAD相等,都为30°,∠CEA=90°,从而求得∠ACE的度数,又因为∠BCE=40°,∠ADB=∠BDE+∠ACE+∠CAD,从而求得∠ADB的度数.
解答 解:∵AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=30°,∠CEA=90°.
∵∠CEA+∠BAC+∠ACE=180°.
∴∠ACE=30°.
∵∠ADB=∠BCE+∠ACE+∠CAD,∠BCE=40°.
∴∠ADB=40°+30°+30°=100°.
故选项A错误,选项B错误,选项C错误,选项D正确.
故选D.
点评 本题考查三角形的内角和、角的平分线、三角形的一个外角等于和它不相邻的内角的和,关键是根据具体目中的信息,灵活变化,求出相应的问题的答案.

练习册系列答案
相关题目
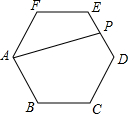 如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长.
如图,在正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,求AP的长.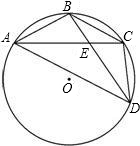 如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.若BE=3,ED=6,则AB=3$\sqrt{3}$.
如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.若BE=3,ED=6,则AB=3$\sqrt{3}$.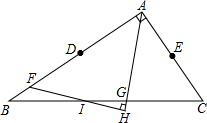 已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI.
已知:△ABC中,D是AB的中点,E是AC的中点,F是DB上的一点,DF=AE,AG是∠BAC的角平分线,FH⊥AG垂足是H,FH、BC相交于I,求证:BI=CI. 如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.
如图,A(3,0),B(0,3),C(1,4),求△ABC的面积.