题目内容
15.把a$\sqrt{-\frac{1}{a}}$中根号外因式适当变形后移至根号内得$\sqrt{-a}$.分析 首先判断出a<0,然后根据二次根式的性质和化简方法,求出把a$\sqrt{-\frac{1}{a}}$中根号外因式适当变形后移至根号内得到的根式即可.
解答 解:∵-$\frac{1}{a}$>0,
∴a<0,
∴a$\sqrt{-\frac{1}{a}}$=$\sqrt{{a}^{2}•(-\frac{1}{a})}$=$\sqrt{-a}$.
故答案为:$\sqrt{-a}$.
点评 此题主要考查了二次根式的性质和化简,要熟练掌握,解答此题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.

练习册系列答案
相关题目
17.等式(-a-3)( )=9-a2中,括号内应填入( )
| A. | a-3 | B. | 3-a | C. | a+3 | D. | -3-a |
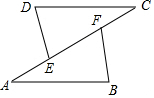 如图,点E,F在AC上,AB=CD,AE=CF,BF=DE,△ABF与△CDE全等吗?说明你的理由.
如图,点E,F在AC上,AB=CD,AE=CF,BF=DE,△ABF与△CDE全等吗?说明你的理由.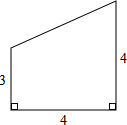 在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的四边形,则原直角三角形纸片的斜边长是10或8$\sqrt{2}$.
在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的四边形,则原直角三角形纸片的斜边长是10或8$\sqrt{2}$.