题目内容
20.在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b(1)若a:c=$\frac{1}{2}$,则a:b=1:$\sqrt{3}$;
(2)若a:b=$\sqrt{2}$:$\sqrt{3}$,c=2$\sqrt{5}$,则b=2$\sqrt{3}$.
分析 (1)设a=k,则c=2k,利用勾股定理求出b的值,即可得到a:b的值;
(2)设a=$\sqrt{2}$k,b=$\sqrt{3}$k,利用勾股定理可得到关于k的方程,解方程即可求出k的值,进而得到b的值.
解答  解:
解:
(1)∵a:c=$\frac{1}{2}$,
∴可设a=k,则c=2k,
∵a2+b2=c2,
∴b=$\sqrt{3}$k,
∴a:b=1:$\sqrt{3}$,
故答案为:1:$\sqrt{3}$;
(2)设a=$\sqrt{2}$k,b=$\sqrt{3}$k,(k>0),
∵a2+b2=c2,c=2$\sqrt{5}$,
∴2k2+3k2=20,
∴k=2,
即b=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查了勾股定理的应用,注意:在直角三角形ABC中∠ACB=90°,两直角边a、b的平方和等于斜边c的平方.

练习册系列答案
相关题目
4.如图,将边长为a的正方形剪去两个小长方形得到S图案,再将这两个小长方形拼成一个新的长方形,求新的长方形的周长( )
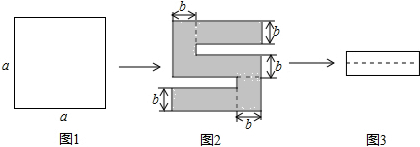

| A. | 2a-3b | B. | 4a-8b | C. | 2a-4b | D. | 4a-16b |
 如图,在∠ABC的内部有一点P,点P到M,N两点的距离相等且到∠ABC两边的距离也相等.请用尺规作图作出点P,不写作法,保留痕迹.
如图,在∠ABC的内部有一点P,点P到M,N两点的距离相等且到∠ABC两边的距离也相等.请用尺规作图作出点P,不写作法,保留痕迹.