题目内容
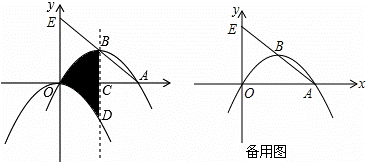
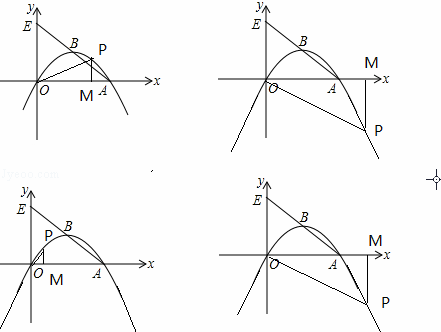
如图,抛物线l1:y=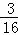 x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.
x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.
(1)求l2的解析式并和阴影部分的面积S阴影;
在l2的对称轴上是否存在一个点F,使得△OEF的周长最小?若存在,求出点F的坐标;若不存在,说明理由;
(3)点P是抛物线l2上一个动点,过P作PM⊥x轴垂足为M,是否存在点P,使得以O、P、M为顶点的三角形与△OAE相似?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
解:(1)设平移后抛物线的解析式y=﹣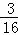 x2+bx,
x2+bx,
将点A(8,0)代入,
得:0=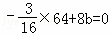 ,
,
解得:b=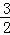 ,∴y=
,∴y=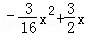 ,
,
顶点B(4,3),
S阴影=OC×CB=4×3=12;
存在,
∵点O与点A关于l2的对称轴对称,
∴连接AE,OF,OF+EF=AE,
此时,点F与点B重合,
∴F(4,3);
(3)存在点P,使得以O、P、M为顶点的三角形与△OAE相似,
设点P(t, ) (t≠0),则:OM=|t|,PM=|
) (t≠0),则:OM=|t|,PM=| |,
|,
设直线AB的解析式为:y=kx+b,
把点A(8,0)和B(4,3)代入可得:
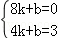 ,
,
解得: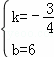 ,
,
∴y=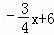 ,当x=0时,y=6,
,当x=0时,y=6,
∴E(0,6),
①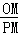 =
=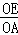 =
=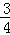 时,
时,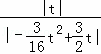 =
=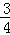 ,
,
∴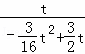 =
=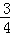 或
或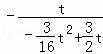 =
=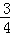 ,
,
解得:t=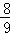 ,或t=
,或t=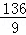 ∴P(
∴P(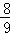 ,
,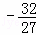 )或P(
)或P(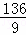 ,
,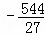 ),
),
②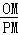 =
=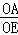 =
=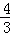 时,
时,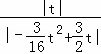 =
=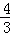 ,
,
∴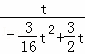 =
=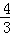 或
或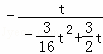 =
=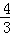 ,
,
解得:t=4或t=12,∴P(4,3)或P(12,﹣9),
∴P1(4,3),P2(12,﹣9),P3(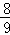 ,
,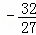 ),P4(
),P4(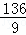 ,
,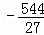 )
)
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,0,
,0, ,
, ,
, ,
, 中,无理数有( )
中,无理数有( )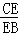 =
= 时,求
时,求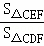 的值;
的值; OA.
OA.

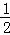 x+b与反比例函数y=
x+b与反比例函数y=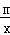 在第二象限的图象交于A(n,
在第二象限的图象交于A(n,

 沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )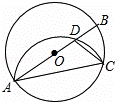
 B.
B.  C.
C.  D.
D. 
