题目内容
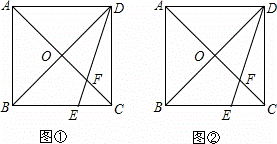
如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.
(1)如图①,当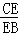 =
= 时,求
时,求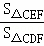 的值;
的值;
(2)如图②,当DE平分∠CDB时,求证:AF= OA.
OA.
(1)解:∵ =
= ,
,
∴ =
= .
.
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,
∴△CEF∽△ADF,
∴ =
= ,
,
∴ =
= =
= ,
,
∴ =
= =
= ;
;
(2)证明:∵DE平分∠CDB,
∴∠ODF=∠CDF,
又∵AC、BD是正方形ABCD的对角线.
∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,
∵∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,
∴AD=AF,
在直角△AOD中,根据勾股定理得:AD= =
= OA,
OA,
∴AF= OA.
OA.

练习册系列答案
相关题目
 中自变量x的取值范围是( )
中自变量x的取值范围是( )
 ﹣
﹣ ,其中a=1.
,其中a=1. B. ﹣1 C. 0 D.
B. ﹣1 C. 0 D. 
 x的图象与x轴正半轴所成的锐角度数是( )
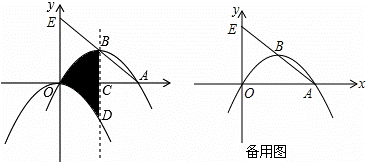
x的图象与x轴正半轴所成的锐角度数是( )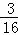 x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.
x2平移后过点A(8,0)和原点得到抛物线l2,l2 的顶点为B,对称轴与x轴相交于点C,与原抛物线l1相交于点D,直线AB交y轴于点E.