题目内容
1．
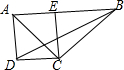如图，在四边形ABCD中，∠A=90°，连接AC、BD，过点C作CE⊥AB，交AB于点E，E恰为AB的中点．若BD平分∠ABC，AC=12cm，AD=5cm，则△BCD的面积为30cm2．
分析 DF⊥BC，交BC延长线于点F，根据BD平分∠ABC可得DF=AD=5cm，再根据CE⊥AB且AE=BE可得AC=BC=12cm，最后由三角形面积公式即可得答案．
解答 解：如图，过点D作DF⊥BC，交BC延长线于点F，
∵BD平分∠ABC，AD=5cm，
∴DF=AD=5cm，
又∵CE⊥AB，且AE=BE，
∴AC=BC=12cm，
∴S△BCD=$\frac{1}{2}$BC•DF=$\frac{1}{2}$×12×5=30（cm2），
故答案为：30cm2．
点评 本题主要考查角平分线的性质和中垂线的性质，熟练掌握角平分线的性质和中垂线的性质是解题的关键．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
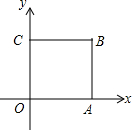如图，在平面直角坐标系xOy中，边长为2的正方形OCBA，点A、C分别在x轴、y轴上，把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1（ 0＜α＜90）﹒
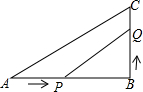如图，在△ABC中，∠B=90°，AB=6cm，点P从点A开始沿AB向B以1cm/s的速度移动，点Q从点B开始沿BC向C点以2cm/s的速度移动，如果P，Q分别从A，B同时出发，2或4秒后△PBQ的面积等于8cm2．