题目内容
11.在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.(1)作出符合本题的几何图形;
(2)求证:BE∥DF.
分析 (1)根据题意画出图形即可;
(2)根据四边形内角和为360°可得∠ADC+∠ABC=180°,然后再根据角平分线定义可得∠ADF=∠FDE=$\frac{1}{2}∠$ADC,∠EBF=∠EBC=$\frac{1}{2}∠$ABC,再证明∠DFA=∠EBF可得结论.
解答 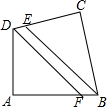 (1)解:如图所示:
(1)解:如图所示:
(2)证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BE平分∠ABC,DF平分∠CDA,
∴∠ADF=∠FDE=$\frac{1}{2}∠$ADC,∠EBF=∠EBC=$\frac{1}{2}∠$ABC,
∴∠FBE+∠FDE=90°,
∵∠A=90°,
∴∠AFD+∠ADF=90°,
∴∠AFD+∠EDF=90°,
∴∠DFA=∠EBF,
∴DF∥EB.
点评 此题主要考查了平行线的判定,以及四边形内角和,关键是掌握同位角相等,两直线平行.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
1.在下列各数中,绝对值最大的数是( )
| A. | -2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
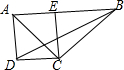 如图,在四边形ABCD中,∠A=90°,连接AC、BD,过点C作CE⊥AB,交AB于点E,E恰为AB的中点.若BD平分∠ABC,AC=12cm,AD=5cm,则△BCD的面积为30cm2.
如图,在四边形ABCD中,∠A=90°,连接AC、BD,过点C作CE⊥AB,交AB于点E,E恰为AB的中点.若BD平分∠ABC,AC=12cm,AD=5cm,则△BCD的面积为30cm2.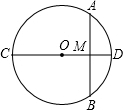 如图,CD是⊙O的直径,CD⊥AB于M,已知AB=8,MO=3,则⊙O的半径为5.
如图,CD是⊙O的直径,CD⊥AB于M,已知AB=8,MO=3,则⊙O的半径为5. 为了改善小区环境,某小区决定要在一块一边靠墙(墙的最大可用长度为10米)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40米的栅栏围住(如图).若设绿化带的BC边长为x米,绿化带的面积为y平方米.
为了改善小区环境,某小区决定要在一块一边靠墙(墙的最大可用长度为10米)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40米的栅栏围住(如图).若设绿化带的BC边长为x米,绿化带的面积为y平方米.