题目内容
1. 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
分析 连接BD,证出△ADE≌△BDF,得到AE=BF,再利用AE=t,CF=2t,则BF=BC-CF=4-2t求出时间t的值.
解答  解:连接BD,
解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=$\frac{1}{2}$∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
∴△ADE和△BDF中,$\left\{\begin{array}{l}{AD=BD}\\{∠A=∠DBC=60°}\\{∠ADE=∠BDF}\end{array}\right.$,
∴△ADE≌△BDF,
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC-CF=4-2t,
∴t=4-2t
∴t=$\frac{4}{3}$
故选D.
点评 本题主要考查了菱形的性质,全等三角形的判定与性质等知识,解题的关键是运用三角形全等得出AE=BF.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.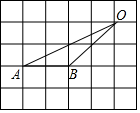 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )
在下列网格中,小正方形的边长为1,点A,B,O都在格点上,求∠A的余弦值( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
13.若关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,那么k的取值范围是( )
| A. | k<0 | B. | k≠0 | C. | k<1 | D. | k>1 |





 (1)解方程:$\frac{1}{x-2}$+$\frac{x+2}{2-x}$=2
(1)解方程:$\frac{1}{x-2}$+$\frac{x+2}{2-x}$=2