题目内容
3.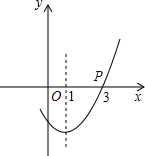 如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥:
如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥:①abc>0
②方程ax2+bx+c=0有两个不相等的实数根
③a-b+c=0
④当x>0时,y随x的增大而增大
⑤不等式ax2+bx+c>0的解为x>3
⑥3a+2c<0.
分析 根据抛物线的图象,数形结合,逐一解析判断,即可解决问题.
解答 解:∵抛物线的对称轴为x=1,抛物线与x轴有两个交点,
∴-$\frac{b}{2a}$=1,b=-2a,另一个交点为(-1,0);
∵抛物线开口向上,
∴a>0,b<0;由图象知c<0,
∴abc>0,故①正确;
由图象知抛物线与x轴有两个交点,
故②正确;
把x=-1代入y=ax2+bx+c=a-b+c=0,故③正确;
由抛物线的对称性及单调性知:x>1时,y随x的增大而增大
故④错误;
不等式ax2+bx+c>0的解为x>3或x<-1,故⑤错误;
⑥由③可知a-b+c=0,
∵b=-2a,a>0,
∴3a+c=0,
∴c=-3a,
∴3a+2c=-3a<0,
故⑥正确.
故答案为:①②③⑥.
点评 该题主要考查了二次函数的图象与系数的关系、抛物线的单调性、对称性及其应用问题;灵活运用有关知识来分析、解答是关键.

练习册系列答案
相关题目
8.直线y=kx+b(k≠0)经过点A(1,m),B(m,1),(m>1),则必有( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
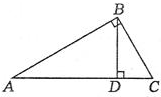 如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.
如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.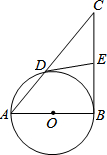 已知:如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,点E是BC的中点,连接DE.
已知:如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,点E是BC的中点,连接DE.