题目内容
12.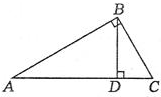 如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.
如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.
分析 先由勾股定理求得DC=3,然后证明△BCD∽△ABD,然后利用相似三角形的面积比等于相似比的平方求解即可,cos∠ABD=cos∠C=$\frac{DC}{BC}$,依据相似三角形的性质可求得AB的长.
解答 解:在Rt△DCB中,DC=$\sqrt{B{C}^{2}-B{D}^{2}}$=3.
∵∠ABC=90°,
∴∠CBD+∠ABD=90°.
∵∠A+∠ABD=90°,
∴∠A=∠DBC.
又∵BD⊥AC,
∴∠BDA=∠BDC.
∴△BCD∽△ABD.
∴$\frac{{S}_{△BCD}}{{S}_{△ABD}}=(\frac{DC}{BD})^{2}$=9:16.
∵∠ABD=∠C,
∴cos∠ABD=cos∠C=$\frac{DC}{BC}$=$\frac{3}{5}$.
∵△BCD∽△ABD,
∴$\frac{AB}{BD}=\frac{BC}{DC}$,即$\frac{AB}{4}=\frac{5}{3}$.
∴AB=$\frac{20}{3}$.
故答案为:9:16;3:5;$\frac{20}{3}$
点评 本题主要考查的是相似三角形的性质和判定、锐角三角函数的定义,掌握相似三角形的性质是解题的关键.

练习册系列答案
相关题目
1.若△MNP≌△NMQ,且MN=8cm,NP=7cm,PM=6cm,则MQ的长为( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
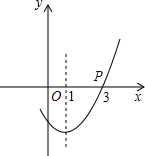 如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥:
如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥: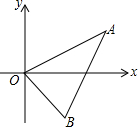 如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).
如图,已知A (4,2),B(2,-2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为(2,1)或(-2,-1).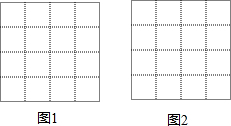 在图1、图2中的每个小正方形的边长都是1.
在图1、图2中的每个小正方形的边长都是1.