题目内容
13.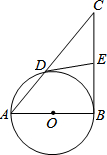 已知:如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,点E是BC的中点,连接DE.
已知:如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,点E是BC的中点,连接DE.(1)DE与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,四边形OBED是正方形?并说明理由.
分析 (1)利用圆周角定理得出∠ADB=90°,进而得出∠EDB=∠EBD,从而得出∠ODE=∠OBD+∠EBD=90°,问题得证;
(2)由题意得出四边形OBED是矩形,即可得出结论.
解答 解:(1)DE与⊙O相切;理由如下: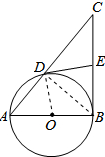
连接OD、BD.
∵AB是⊙O的直径,
∴∠ADB=90°,
则∠CDB=90°,
点E为BC的中点,
∴ED=$\frac{1}{2}$BC=EB,
∴∠EDB=∠EBD,
∵OB=OD,
∴∠ODB=∠OBD,
∴∠ODE=∠OBD+∠EBD=90°,
∴DE是⊙O的切线;
(2)当∠A=∠C=45°时,四边形OBED是正方形.理由如下:
∵∠A=45°时,OA=OD,
∴∠DOB=90°
∴∠DOB=∠OBE=∠ODE=90°,
∴四边形OBED是矩形.
又∵OB=OD,
∴四边形OBED是正方形
点评 此题主要考查了切线的判定定理、圆周角定理、正方形的判定方法、矩形的判定方法、等腰三角形的性质、直角三角形斜边上的中线性质;熟练掌握切线的判定定理,证明四边形OBED是矩形是解决(2)的关键.

练习册系列答案
相关题目
1.若△MNP≌△NMQ,且MN=8cm,NP=7cm,PM=6cm,则MQ的长为( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
18.抛物线y=x2不具有的性质是( )
| A. | 对称轴是y轴 | B. | 开口向上 | ||
| C. | 当x<0时,y随x的增大而增大 | D. | 顶点坐标是(0,0) |
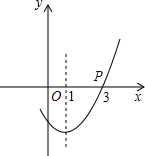 如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥:
如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥: 已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB 于D、E,△ABE的周长等于29cm,则EC的长为3.5cm.
已知:如图,AB=AC=12cm,AB的垂直平分线分别交AC、AB 于D、E,△ABE的周长等于29cm,则EC的长为3.5cm.