题目内容
14.解方程:(1)(x-2)2-25=0;
(2)3(x-2)2=x(x-2);
(3)2x2-x-1=0;
(4)x2+2x-3=0(配方法).
分析 (1)方程移项后,利用直接开平方法求出解即可;
(2)方程移项后,利用因式分解法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程利用配方法求出解即可.
解答 解:(1)方程整理得:(x-2)2=25,
开方得:x-2=5或x-2=-5,
解得:x1=7,x2=-3;
(2)方程移项得:3(x-2)2-x(x-2)=0,
分解因式得:(x-2)(3x-6-x)=0,
解得:x1=2,x2=3;
(3)分解因式得:(2x+1)(x-1)=0,
解得:x1=-$\frac{1}{2}$,x2=2;
(4)移项得:x2+2x=3,
配方得:x2+2x+1=4,即(x+1)2=4,
开方得:x+1=2或x+1=-2,
解得:x1=1,x2=-3.
点评 此题考查了解一元二次方程-因式分解法,配方法,直接开平方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
19.阅读下面材料,在数学课上,老师提出如下问题:
小颢这样操作的:
老师说:“小颢的做法是正确的.”
请回答:小颢的作图依据是对角线互相垂直平分的四边形是菱形.
| 已知:线段AB. 尺规作图:以线段AB为对角线作一个菱形ADBC. |
| 如图:(1)分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于C、D; (2)作四边形ADBC. 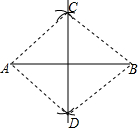 |
请回答:小颢的作图依据是对角线互相垂直平分的四边形是菱形.
6.某药品经过两次降价,每瓶零售价由100元降为81元,已知两次降价的百分率x都相同,那么x是( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
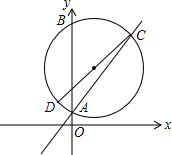 如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.
如图,半径为5的⊙O1,交直线y=x+2于A(0,2),C两点,交y轴与B(0,10),CD是⊙O1的直径,若函数y=$\frac{k}{x}$(x<0)的图象经过点D,求k的值.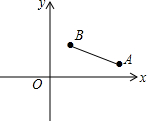 如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.
如图,在平面直角坐标系中,已知A(a,1),B(2,b),且a,b满足(2a-3b-2)2+$\sqrt{a-2b}$=0.
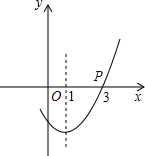 如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥:
如图是抛物线y=ax2+bx+c的一部分,且其过点(3,0),对称轴为直线x=1,则下列结论正确的有①②③⑥: