题目内容
11.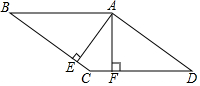 已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.
已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.
分析 在四边形AECF中由∠EAF=30°得∠BCD=150°,根据平行四边形的性质得∠D=∠B=180°-∠BCD=30°,根据直角三角形的性质可得AB=2AE=7、AD=2AF=5.6,由直线间的距离及平行四边形面积公式可得答案.
解答 解:∵AE⊥BC,AF⊥DC,
∴∠AEC=∠AFC=90°,
∵∠EAF=30°,
∴∠BCD=360°-∠AEC-∠AFC-∠EAF=150°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠D=∠B=180°-∠BCD=30°,
在Rt△ABE中,∵AE=3.5,
∴AB=2AE=7,
在Rt△ADF中,∵AF=2.8,
∴AD=2AF=5.6,
BC与AD间的距离是3.5,S?ABCD=BC•AE=AD•AE=5.6×3.5=19.6,
故答案为:7,5.6,3.5,19.6.
点评 本题主要考查平行四边形的性质,熟练掌握四边形内角和、平行四边形的性质、直角三角形的性质及平行四边形的面积公式是解题的关键.

练习册系列答案
相关题目
16.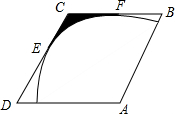 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
1.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
| A. | 0≤b<2$\sqrt{2}$ | B. | -2$\sqrt{2}≤b≤2\sqrt{2}$ | C. | -2$\sqrt{3}<b<$2$\sqrt{3}$ | D. | -2$\sqrt{2}$<b<2$\sqrt{2}$ |
 完成下列推理过程
完成下列推理过程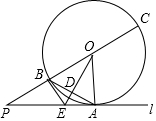 如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
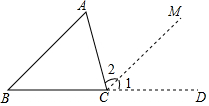
如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.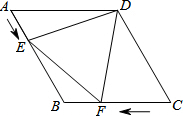 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
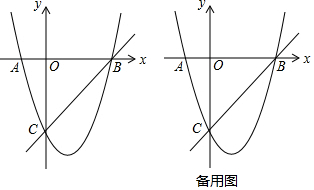
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( ) 在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).
在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).