题目内容
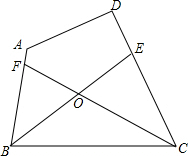 已知如图,在四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.
已知如图,在四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.考点:多边形内角与外角
专题:
分析:先根据四边形内角和等于360°和已知条件求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和外角的关系即可求得∠BOF的度数.
解答:解:∵四边形ABCD中,∠A=124°,∠D=100°,
∴∠ABC+∠BCD=360°-(∠A+∠D)=136°,
∵∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,
∴∠OBC+∠OCB=
(∠ABC+∠BCD)=68°,
则∠BOF=∠OBC+∠OCB=68°.
∴∠ABC+∠BCD=360°-(∠A+∠D)=136°,
∵∠ABC的平分线BE交CD于E,∠BCD的平分线CE交AB于F,
∴∠OBC+∠OCB=
| 1 |
| 2 |
则∠BOF=∠OBC+∠OCB=68°.
点评:本题考查了多边形的内角和外角,三角形的内角和定理,关键是得到∠ABC+∠BCD的度数,注意整体思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC中,AB=AC,BC=8,其外接圆半径为5,则△ABC的周长为( )
A、8+4
| ||||
B、8+8
| ||||
C、8+4
| ||||
| D、以上都不对 |
三棱柱共有( )
| A、3条棱 | B、6条棱 |
| C、9条棱 | D、12条棱 |
 探索活动:观察图中∠1和∠2的位置特点?
探索活动:观察图中∠1和∠2的位置特点? 如图,点P是反比例函数y=
如图,点P是反比例函数y= 将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.
将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.