题目内容
 如图,在边长为a的等边三角形ABC中作内接矩形EFGH,使FG在BC边上,点E,H分别在AB,AC边上,求这个矩形面积S的最大值.
如图,在边长为a的等边三角形ABC中作内接矩形EFGH,使FG在BC边上,点E,H分别在AB,AC边上,求这个矩形面积S的最大值.考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:如图,作辅助线;求出AN=
a,AM=
a-λ;证明△AEH∽△ABC,求出EH=a-
λ,S=λ(a-
λ)=-
λ2+aλ,即可解决问题.
| ||
| 2 |
| ||
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
解答: 解:如图,过点A作AN⊥BC于点N,交EH于点M;
解:如图,过点A作AN⊥BC于点N,交EH于点M;
∵四边形EFGH为矩形,
∴EF=MN(设为λ),EH∥BC;
∵△ABC是边长为a的等边三角形,
∴∠B=60°,sin60°=
,
∴AN=
a,AM=
a-λ;
∵EH∥BC,
∴△AEH∽△ABC,
∴
=
,
解得EH=a-
λ,
∴S=λ(a-
λ)
=-
λ2+aλ,
∴S的最大值为Smax=
=
a2.
 解:如图,过点A作AN⊥BC于点N,交EH于点M;
解:如图,过点A作AN⊥BC于点N,交EH于点M;∵四边形EFGH为矩形,
∴EF=MN(设为λ),EH∥BC;
∵△ABC是边长为a的等边三角形,
∴∠B=60°,sin60°=
| AN |
| AB |
∴AN=
| ||
| 2 |
| ||
| 2 |
∵EH∥BC,
∴△AEH∽△ABC,
∴
| AM |
| AN |
| EH |
| BC |
解得EH=a-
2
| ||
| 3 |
∴S=λ(a-
2
| ||
| 3 |
=-
2
| ||
| 3 |
∴S的最大值为Smax=
| -a2 | ||||
4×(-
|
| ||
| 8 |
点评:该题主要考查了相似三角形的判定及其性质、二次函数的最值公式及其应用等知识点问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目


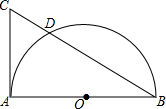 如图,AB是⊙O的直径,CA切⊙O于点A,CD=1cm,DB=3cm,求AB的长.
如图,AB是⊙O的直径,CA切⊙O于点A,CD=1cm,DB=3cm,求AB的长.