题目内容
10.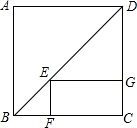 如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
分析 由正方形的性质和已知条件得出BC+CE=10cm,再由矩形的性质易得△BEF与△DEG是等腰直角三角形,继而求得答案.
解答 解:∵四边形ABCD是正方形,
∴∠A=90°,AB=BC=CD=AD,
∵BD=10$\sqrt{2}$cm,
∴BC=CD=AB=AD=10cm,
∴BC+CD=20(cm),
∵四边形EFCG是矩形,
∴∠EFB=∠EGD=90°,
∴△BEF与△DEG是等腰直角三角形,
∴BF=EF,EG=DG,
∴矩形EFCG的周长是:EF+FC+CG+EG=BF+FC+CG+DG=BC+CD=20(cm).
故答案为:20cm.
点评 此题考查了正方形的性质以及矩形的性质、勾股定理.此题难度不大,注意掌握转化思想的应用.

练习册系列答案
相关题目
5.二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
(1)ac<0;(2)当x>1时,y的值随x值得增大而增大;(3)-1是方程ax2+bx+c=0的一个根;(4)当-1<x<2时,ax2+bx+c<0,其中正确的个数为( )
| x | … | 0 | 1 | 2 | … |
| y | … | 4 | -4 | 6 | … |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.如果a与-$\sqrt{5}$互为相反数,则a的值是( )
| A. | 5 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | ±$\sqrt{5}$ |
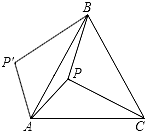 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$. 请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.
请建立适当的平面直角坐标系,写出边长为4的等边△ABC的各顶点坐标.