题目内容
5.二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:| x | … | 0 | 1 | 2 | … |
| y | … | 4 | -4 | 6 | … |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 利用表格中数据得出抛物线的解析式,根据对称轴以及与坐标轴交点,进而分别对每一项进行判断即可得出答案.
解答 解:将(0,4)(1,-4)(2,6)代入y=ax2+bx+c,得:
$\left\{\begin{array}{l}{c=4}\\{a+b+c=-4}\\{4a+2b+c=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=9}\\{b=-17}\\{c=4}\end{array}\right.$
则函数的解析式为:y=9x2-17x+4,
(1)ac=4×9=36>0,故(1)错误;
(2)当x>-$\frac{b}{2a}$=$\frac{17}{18}$时,y的值随x值得增大而增大,故(2)错误;
(3)-1不是方程9x2-17x+4=0的一个根,故(3)错误;
(4)当-1<x<2时,ax2+bx+c<0,故(4)正确;
故选D.
点评 此题考查了二次函数的图象与性质,解答该题时,充分利用了二次函数图象,求出二次函数的解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
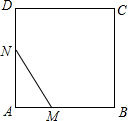 如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.
如图,已知线段AB长度是4,以AB为边作正方形ABCD,动点M,N在正方形的边上运动,且MN=3,如果点M从点A出发,沿着A→B→C→D→A的路线,向点A运动,则点M从点A运动一周回到点A的运动过程中,MN的中点P所经过的路线长度是3π+4.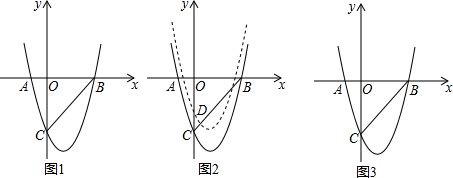
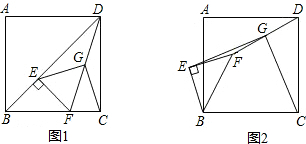
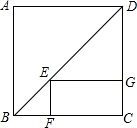 如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.
如图,已知正方形ABCD的一条对角线长为10$\sqrt{2}$cm,矩形EFCG的3个顶点分别在△BCD的边上.则矩形EFCG的周长是20cm.