题目内容
1.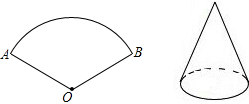 如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm.
如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm.
分析 设圆锥形纸帽的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式得到$\frac{1}{2}$•2πr•18=108π,解得r=6,然后根据勾股定理计算圆锥形纸帽的高.
解答 解:设圆锥形纸帽的底面圆的半径为r,
根据题意得$\frac{1}{2}$•2πr•18=108π,解得r=6,
所以圆锥形纸帽的高=$\sqrt{1{8}^{2}-{6}^{2}}$=12$\sqrt{2}$(cm).
故答案为12$\sqrt{2}$cm.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,已知A(-4,$\frac{1}{2}$),B(n,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(n,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.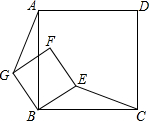 如图,正方形ABCD和正方形GBEF,连接AG、CE,猜想CE与AG的位置关系,并证明你的猜想.
如图,正方形ABCD和正方形GBEF,连接AG、CE,猜想CE与AG的位置关系,并证明你的猜想. 如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,
如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,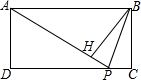 如图,在矩形ABCD中,AP=DC,PH=PC,求证:PB平分∠CBH.
如图,在矩形ABCD中,AP=DC,PH=PC,求证:PB平分∠CBH. 如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.
如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.