题目内容
3.经过已知点M和N的圆的圆心的轨迹是线段MN的垂直平分线.分析 要求作经过已知点M和点N的圆的圆心,则圆心应满足到点M和点N的距离相等,从而根据线段的垂直平分线性质即可求解.
解答 解:根据同圆的半径相等,则圆心应满足到点M和点N的距离相等,即经过已知点M和点N的圆的圆心的轨迹是线段MN的垂直平分线.
故答案为:线段MN的垂直平分线.
点评 此题考查了点的轨迹问题,熟悉线段垂直平分线的性质是解题关键.

练习册系列答案
相关题目
11. 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
8.观察下列4个命题:
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
13.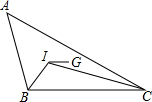 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
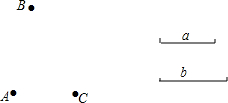 如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.
如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.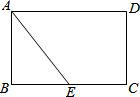 如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.
如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是$\frac{18}{5}$ cm.