题目内容
7.在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果当 x≥0时,y′=y;当 x<0时,y′=-y,那么称点Q为点P的“关联点”.例如:点(-5,6)的“关联点”为(-5,-6).如果点N(n+1,2)是一次函数y=x+3图象上点M的“关联点”,则点M的坐标为(-5,-2).
分析 分n+1≥0或n+1<0两种情况,根据“关联点”的定义找出点M的坐标,利用一次函数图象上点的坐标特征求出n+1的值,比照后即可得出结论.
解答 解:当n+1≥0时,点M为(n+1,2),
∴n+1+3=2,
∴n+1=-1,与n+1>0冲突,故舍去;
当n+1<0时,点M为(n+1,-2),
∴n+1+3=-2,
∴n+1=-5,
∴点M的坐标为(-5,-2).
故答案为:(-5,-2).
点评 本题考查了一次函数图象上点的坐标特征,分n+1≥0或n+1<0两种情况寻找点M的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.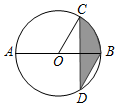 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )| A. | 4π | B. | 2π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{4}$ |
2.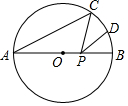 如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
 如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}-1$ |
9.有4根小棒,长度分别为2cm、3cm、4cm、5cm任意取3根小棒首尾顺次相接搭三角,可以撘出不同的三角形的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{6}$=3 | B. | $\sqrt{2}$×$\sqrt{6}$=3$\sqrt{2}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | ($\sqrt{12}$-$\sqrt{3}$)×$\sqrt{3}$=3 |


 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m,8m,现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩建后的等腰三角形花圃的周长.