题目内容
14.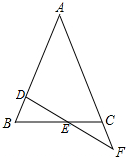 如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?
如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?
分析 作DG∥AF交BC于G,则∠DGB=∠ACB,∠GDE=∠CFE,由等腰三角形的性质得出∠B=∠ACB,证出GD=CF,由AAS证明△DGE≌△FCE,得出对应边相等DE=FE,即可得出结论.
解答 解:能证明;理由如下: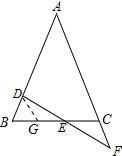
作DG∥AF交BC于G,如图所示:
则∠DGB=∠ACB,∠GDE=∠CFE,
∵AB=AC,
∴∠B=∠ACB,
∴∠DGB=∠B,
∴BD=GD,
∵BD=CF,
∴GD=CF,
在△DGE和△FCE中,$\left\{\begin{array}{l}{∠GDE=∠FCE}&{\;}\\{∠DEG=∠FEC}&{\;}\\{GD=CF}&{\;}\end{array}\right.$,
∴△DGE≌△FCE(AAS),
∴DE=FE,
即E是DF的中点.
点评 本题考查了等腰三角形的性质与判定、全等三角形的判定与性质、平行线的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.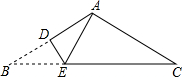 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
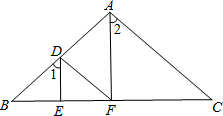 如图,已知DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试判断AC与DF的关系,并说明理由.
如图,已知DE平分∠BDF,AF平分∠BAC,且∠1=∠2,试判断AC与DF的关系,并说明理由.