题目内容
17．
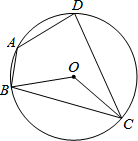如图，圆O的内接四边形ABCD中，BC=DC，∠BOC=130°，则∠BAD的度数是（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 150° |
分析 根据圆心角、弧、弦的关系由BC=DC得$\widehat{BC}$=$\widehat{DC}$，则∠BOC=∠COD=130°，再利用周角定义计算出∠BOD=100°，再根据圆周角定理得到∠BCD=$\frac{1}{2}$∠BOD=50°，然后根据圆内接四边形的性质计算∠BAD的度数．
解答 
解：连结OD，如图，
∵BC=DC，
∴$\widehat{BC}$=$\widehat{DC}$，
∴∠BOC=∠COD=130°，
∴∠BOD=360°-2×130°=100°，
∴∠BCD=$\frac{1}{2}$∠BOD=50°，
∴∠BAD=180°-∠BCD=180°-50°=130°．
故选B．
点评 本题考查了圆内接四边形的性质：圆内接四边形的对角互补；圆内接四边形的任意一个外角等于它的内对角（就是和它相邻的内角的对角）．也考查了圆心角、弧、弦的关系．
练习册系列答案
相关题目
如图，在△ABC中，已知AB=AC，CE⊥BD，CD=CB，求证：
8．某公司的物流业务原来由A运输队承接，已知其收费标准y（元）与运输所跑路程x（公里）之间是某种函数关系．其中部分数据如表所示：
（1）写出y（元）关于x（公里）的函数解析式yA=2.5x；（不需写出定义域）
（2）由于行业竞争激烈，现B运输队表示：若公司每次支付200元的汽车租赁费，则可按每公里0.9元收费．请写出B运输队每次收费y（元）关于所跑路程x（公里）的函数解析式yB=200+0.9x；（不需写出定义域）
（3）如果该公司有一笔路程500公里的运输业务，请通过计算说明应该选择哪家运输队？
| x（公里） | 80 | 120 | 180 | 200 | … |
| y（元） | 200 | 300 | 450 | 500 | … |
（2）由于行业竞争激烈，现B运输队表示：若公司每次支付200元的汽车租赁费，则可按每公里0.9元收费．请写出B运输队每次收费y（元）关于所跑路程x（公里）的函数解析式yB=200+0.9x；（不需写出定义域）
（3）如果该公司有一笔路程500公里的运输业务，请通过计算说明应该选择哪家运输队？
5．
如图所示的立体图形，它的主视图是（ ）
如图所示的立体图形，它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
12．下列四个数中，值最小的数是（ ）
| A． | tan45° | B． | $\sqrt{3}$ | C． | π | D． | $\frac{8}{3}$ |
如图，已知抛物线y=x2-2x+2与y轴交于点A．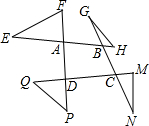
如图，以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ，求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数．
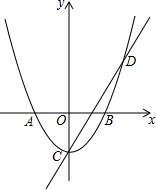如图，在平面直角坐标系中，抛物线与x轴交于点A（-1，0）和点B（1，0），直线y=2x-1与y轴交于点C，与抛物线交于点C、D．