题目内容
2. 如图,已知抛物线y=x2-2x+2与y轴交于点A.
如图,已知抛物线y=x2-2x+2与y轴交于点A.(1)平移该抛物线使其经过点A和点B(1,0),求平移后的抛物线解析式.
(2)求该抛物线的对称轴与(1)中平移后的抛物线对称轴之间的距离.
分析 (1)根据平移规律,可得函数解析式,根据图象上的点满足函数解析式,可得方程组,根据解方程组,可得答案;
(2)对称轴x=-$\frac{b}{2a}$,可得函数解析式的对称轴,根据平行间的距离,可得答案.
解答 解:(1)设平移后的函数解析式为y=(x+a)2-2(x+a)+2+b,
将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{{a}^{2}-2a+2+b=2}\\{(a+1)^{2}-2(a+1)+2+b=0}\end{array}\right.$,
解$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{3}{4}}\end{array}\right.$,
平移后的解析式为y=x2-x+2;
(2)平移前的对称轴是x=1,平移后的对称轴是x=$\frac{1}{2}$,
抛物线的对称轴与(1)中平移后的抛物线对称轴之间的距离1-$\frac{1}{2}$=$\frac{1}{2}$.
点评 本题考查了二次函数图象与几何变换,函数图象左移加,右移减,上移加,下移减.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | (-2)3=8 | B. | ($\frac{1}{3}$)-1=3 | C. | a4•a2=a8 | D. | a6÷a3=a2 |
17.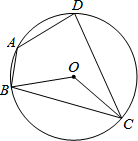 如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )
如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )
 如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )
如图,圆O的内接四边形ABCD中,BC=DC,∠BOC=130°,则∠BAD的度数是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
 如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.
如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.