如图.Rt△ABC中.∠C=90°.AB边上的中垂线分别交BC.AB于点D.E.若AE=AC=4cm.△ADC的周长为4$\sqrt{3}$+4cm．题目和参考答案——青夏教育精英家教网—

题目内容

11．

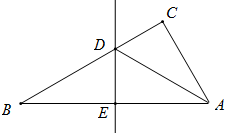如图，Rt△ABC中，∠C=90°，AB边上的中垂线分别交BC、AB于点D、E，若AE=AC=4cm，△ADC的周长为4$\sqrt{3}$+4cm．

分析根据线段垂直平分线的概念和性质得到AD=BD，AB=2AE=8cm，根据勾股定理求出BC，根据三角形的周长公式计算即可．

解答解：∵DE是AB的垂直平分线，AE=4cm，
∴AD=BD，AB=2AE=8cm，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4$\sqrt{3}$cm，
∴△ADC的周长为：AD+CD+AC=BD+CD+AC=BC+AC=（4$\sqrt{3}$+4）cm，
故答案为：4$\sqrt{3}$+4．

点评本题考查的是线段的垂直平分线的概念和性质，线段的垂直平分线上的点到线段的两个端点的距离相等．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

16．计算：
（1）$\sqrt{（\sqrt{2}-\sqrt{3）^{2}}}$-2|$\sqrt{2}$-$\sqrt{3}$|-|-$\sqrt{3}$|；
（2）$\root{3}{（-1）^{2}}$+$\root{3}{-8}$-|1-$\sqrt{3}$|；
（3）$\root{3}{\frac{1}{8}}$-$\frac{5}{2}$$\root{3}{-\frac{1}{125}}$+$\root{3}{-343}$-$\root{3}{27}$．

13．

如图，等腰三角形ABC中，∠AC=90°，D，E分别为AB，AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD，交BE于点G，交AC于点M．
（1）求证：GM=GE；
（2）求证：BG=AF+FG．

6．

如图，一个5×5的网格ABCD，在其形内有16个网格交点，分别以A、C为圆心，AB长（5个单位）为半径在形内画弧，两弧相交于点B、D，那么上述16个网格交点中位于两弧之间（不含弧上）的有（　　）

	A．	两个矩形		B．	两个等边三角形
	C．	各有一角是80°的两个等腰三角形		D．	任意两个菱形

3．下列哪个条件不能判定两直线平行（　　）

20．已知n是奇数，m是偶数，关于x，y的二元一次方程组$\left\{\begin{array}{l}{2014x+15y=n}\\{2015x+18y=m}\end{array}\right.$，有整数解$\left\{\begin{array}{l}{x={x}_{0}}\\{y={y}_{0}}\end{array}\right.$，则（　　）

	A．	x₀，y₀均为偶数		B．	x₀，y₀均为奇数
	C．	x₀是偶数，y₀是奇数		D．	x₀是奇数，y₀是偶数

1．现测得甲、乙、丙、丁四位学生身高分别如下：156cm，159cm，152cm，157cm．
（1）求这四位学生身高的平均值；
（2）以计算的平均值为标准，用正数表示超出部分，用负数表示不足部分，这四位学生的身高应分别记为多少？
（3）若甲的身高记为-2cm，请在图中的数轴上用点A，B，C，D分别表示甲、乙、丙、丁这四位学生的身高．

试题分类