题目内容
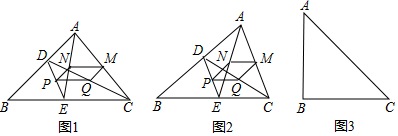
10.如图1,△ABC中,点D、E分别是AB、BC边上点,连结DE、AE、CD,P、Q、M、N分别是DE、CD、AC、AE的中点,顺次连接P、Q、M、N得四边形PQMN.(1)判定四边形PQMN的形状并证明你的结论:
(2)若BD=BE,AB=BC,判定四边形PQMN的形状并证明你的结论:
(3)在(2)的条件下,如果∠B=90°,请在图3中画出符合条件的图形,并直接写出此时四边形PQMN的形状.
分析 (1)由P、Q分别是DE、DC的中点、M、N分别是AC、AE的中点知PQ∥EC且PQ=$\frac{1}{2}$EC、MN∥EC且MN=$\frac{1}{2}$EC,从而得PQ∥MN且PQ=MN,即可得出四边形PQMN是平行四边形;
(2)在(1)的基础上,由BD=BE、AB=BC知AD=EC,从而由得PN=$\frac{1}{2}$AD、PQ=$\frac{1}{2}$EC得PN=PQ,即可得出四边形PQMN是菱形;
(3)在(1)的基础上,由MN∥BC、MQ∥AB知MN⊥MQ,即∠NMQ=90°,即可得四边形PQMN是矩形.
解答 解:(1)∵P、Q分别是DE、DC的中点,
∴PQ是△DEC的中位线,
∴PQ∥EC,且PQ=$\frac{1}{2}$EC,
∵M、N分别是AC、AE的中点,
∴MN是△AEC的中位线,
∴MN∥EC,且MN=$\frac{1}{2}$EC,
∴PQ∥MN,且PQ=MN,
∴四边形PQMN是平行四边形;
(2)四边形PQMN是菱形,
∵P、N分别是DE、AE的中点,P、Q是DE、DC的中点,
∴PN是△DEA的中位线,PQ是△DEC的中位线,
∴PN=$\frac{1}{2}$AD、PQ=$\frac{1}{2}$EC,
∵BD=BE、AB=BC,
∴AB-BD=BC-BE,即AD=EC,
∴PN=PQ,
由(1)知四边形PQMN是平行四边形,
∴四边形PQMN是菱形;
(3)四边形PQMN是矩形,
∵∠B=90°,
∴AB⊥BC,
∵MN∥BC,MQ∥AB,
∴MN⊥MQ,
∴∠NMQ=90°,
∵由(1)知四边形PQMN是平行四边形,
∴四边形PQMN是矩形.
点评 本题考查了矩形的判定、菱形的判定、平行四边形的判定、三角形中位线定理;熟练掌握三角形的中位线定理与矩形、菱形与平行四边形间的联系是解决问题的关键.

| A. | (-a+b)(a-b) | B. | (a-b)(a-2b) | C. | (x+1)(x-1) | D. | (-m-n)(m+n) |
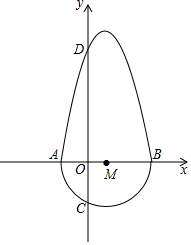 定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.
定义:把一个半圆与抛物线的一部分合成封闭图形,我们把这个封闭图形称为“蛋圆”.如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,8),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为3.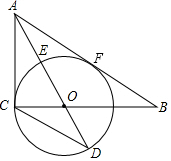 如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.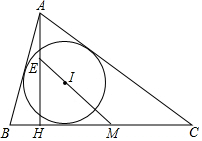 在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径.
在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径.