题目内容
15.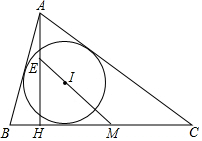 在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径.
在△ABC中,M是BC边的中点,I是内切圆的圆心,AH⊥BC于点H,E是直线IM与AH的交点,求证:AE=r.其中r是内切圆的半径.
分析 设圆I与BC相切于P,连接IP,设AB=c,AC=b,BC=a,根据已知条件得到BM=$\frac{a}{2}$,根据切线的性质得到PB=$\frac{a+c-b}{2}$,根据三角函数的定义得到BH=c•cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}$,根据相似三角形的性质得到EH=r•$\frac{b+c}{a}$①
根据三角形的面积公式得到AH=$\frac{a+b+c}{a}$•r②,于是得到结论.
解答 证明: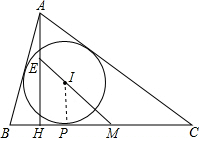 设圆I与BC相切于P,连接IP,
设圆I与BC相切于P,连接IP,
设AB=c,AC=b,BC=a,
则BM=$\frac{a}{2}$,PB=$\frac{a+c-b}{2}$,BH=c•cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}$,
∵△IPM∽△MEH,
∴$\frac{IH}{IP}$=$\frac{HM}{PM}$=$\frac{BM-BH}{BM-BP}$=$\frac{\frac{{a}^{2}}{2}-\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}}{\frac{a}{2}-\frac{a+c-b}{2}}$=$\frac{b+c}{a}$,
∴EH=r•$\frac{b+c}{a}$①
三角形的面积公式知a•AH=(a+b+c),
∴AH=$\frac{a+b+c}{a}$•r②,
结合①,②可得AE=AH-EH=$\frac{a+b+c}{a}$•r-r•$\frac{b+c}{a}$=r
点评 本题考查了三角形的内切圆与内心,相似三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
5.从有关方面获悉,从今年开始,在我市新成立的两江新区的广大农村准备实行农村新型合作医疗保险制度,享受医保的农民可在规定的医院就医并按照规定标准报销部分医疗费用.如表是医疗费用报销的标准:
(说明:住院医疗费用的报销分段计算,如:某人住院医疗费用共30000元,则4000元按40%报销,16000元按a%报销,余下的10000元按60%报销,题中涉及到的医疗费均指允许报销的医疗费)
(1)某农民在2010年门诊看病自己共支付医疗费270元,则他在这一年中门诊医疗费用450元;
(2)已知农民张大爷一年中住院的实际医疗费用为18000元,按标准可报销7900元,求a的值;
(3)若某农民一年中住院的实际医疗费用为x元(4001≤x≤20000),按标准报销的金额为y元,试用x的式子表示y;
(4)若李大叔一年内本人自负住院费18400元(自付医疗费=实际医疗费-按标准报销的金额),则李大叔这一年实际医疗费用共多少?
| 医疗费用 | 门诊 | 住院 | ||
| 0-4000元 | 4001-20000元 | 20000以上 | ||
| 每年报销比例标准 | 40% | 40% | a% | 60% |
(1)某农民在2010年门诊看病自己共支付医疗费270元,则他在这一年中门诊医疗费用450元;
(2)已知农民张大爷一年中住院的实际医疗费用为18000元,按标准可报销7900元,求a的值;
(3)若某农民一年中住院的实际医疗费用为x元(4001≤x≤20000),按标准报销的金额为y元,试用x的式子表示y;
(4)若李大叔一年内本人自负住院费18400元(自付医疗费=实际医疗费-按标准报销的金额),则李大叔这一年实际医疗费用共多少?
7.已知点P(x,y),且|x-2|+|y+4|=0,则点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.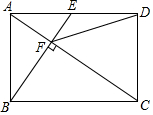 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.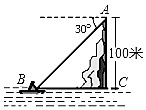 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )| A. | 50$\sqrt{3}$ | B. | 100 | C. | 100+$\sqrt{3}$ | D. | 100$\sqrt{3}$ |
 已知:如图,∠1=72°,∠2=62°,∠3=62°,求∠4=108°.
已知:如图,∠1=72°,∠2=62°,∠3=62°,求∠4=108°.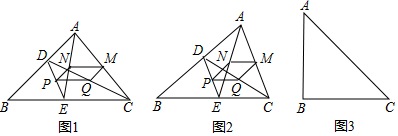
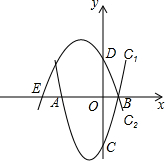 已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).
已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).