题目内容
5.我们把分子为1的分数叫做单位分数,如$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,$\frac{1}{4}$=$\frac{1}{5}$+$\frac{1}{20}$,…(1)根据对上述式子的观察,如果单位分数$\frac{1}{5}$=$\frac{1}{6}$+$\frac{1}{a}$,$\frac{1}{7}$=$\frac{1}{b}$-$\frac{1}{42}$那么a=30b=6;
(2)进一步思考,单位分数$\frac{1}{n}$=$\frac{1}{n+1}$+$\frac{1}{x}$,(n是不小于2的正整数)则x=n(n+1)(用n的代数式表示),并对等式加以验证.
分析 (1)根据所给的式子,观察分母发现2×3=6;3×4=12;4×5=20,可得a=5×6=30;b=42÷7=6;
(2)利用(1)中发现的规律可知x=n(n+1),利用分式的加法整理等式的右边可证得结果.
解答 解:(1)∵$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,$\frac{1}{4}$=$\frac{1}{5}$+$\frac{1}{20}$,…
发现分母间关系:2×3=6;3×4=12;4×5=20,…
∴a=5×6=30;b=42÷7=6;
故答案为:30,6;
(2)利用(1)中发现的规律可知x=n(n+1),
∵右边=$\frac{1}{n+1}+\frac{1}{n(n+1)}$=$\frac{n}{n(n+1)}$$+\frac{1}{n(n+1)}$=$\frac{n+1}{n(n+1)}$=$\frac{1}{n}$=左边
∴等式成立.
故答案为:n(n+1).
点评 本题主要考查了式子的变化规律,根据所给式子发现分母间的关系是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
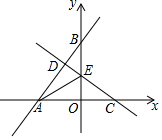 如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
如图,直线l1:y=$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:y=-$\frac{3}{4}$x+b经过点C,且与直线l1交于点D,与y轴交于点E,连结AE. 如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若AC+BD=22cm,△OAB的周长是16cm,则EF的长为2.5cm.
如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若AC+BD=22cm,△OAB的周长是16cm,则EF的长为2.5cm.